Research Results
Software framework for massively parallel computations using the Combination Technique
In order to apply and test the combination technique on GENE, we have developed two software tools. A Python interface, which provides an easy access to GENE used for prototyping and testing, and a generic C++ framework intended for massively parallel simulations with GENE, but also with other parallel codes.In the Python interface, we implemented the standard combination technique, fault-tolerant algorithms, and eigenvalue OptiCom techniques. That interface can be easily used for developing advanced combination technique schemes, and serves as a framework for testing them on small and medium sized GENE computations.
Our C++ framework efficiently runs time-dependent initial value computa- tions with GENE on massively parallel HPC systems, but also supports other application codes. It is part of the part sparse grid software library SG++. The framework implements the manager- worker pattern: The available compute resources, in the form of MPI processes, are arranged in process groups. A central manager process distributes the par- tial problems to the process groups. Each process group executes an instance of the application, e.g. GENE, in order to compute the partial problems assigned to it. The framework already successfully employs the communica- tion schemes and load-balancing techniques presented below and will be extended to include fault tolerance techniques, as well as support the optimized combination technique and the iterated defect correction.
Exa-challenges and solutions: Scalability
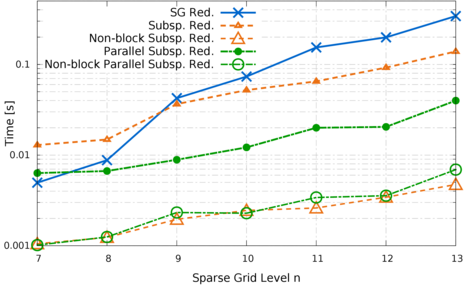
The coarse (second) level of parallelization decouples the original full-grid problem into many smaller, fully independent anisotropic subproblems, which are finally combined into one solution. In time-dependent computations, the corresponding partial solutions are recombined every few timesteps to avoid divergence. Even when divergence is not an issue, it might be necessary to calculate the combination solution every few timesteps to trace certain aspects of the solution field over time. For initial value simulation with GENE, for example, a typical quantity of interest is the evolution of the particles' distribution functions. The recombination requires global communication steps, which might affect the scalability on large parallel systems.To solve this issue, we have developed global communication schemes for the combination technique that minimize the communication time by exploiting the hierarchical structure of the combination solution. Experiments on 456 nodes of the supercomputer Hermit (HLRS) were performed for different implementations of these schemes. A five-dimensional test problem was discretized up to level 13. Using the non-blocking collective operations of the MPI 3.0 standard, we could confirm a reduction in communication time of up to a factor of 72, compared to the naive algorithm
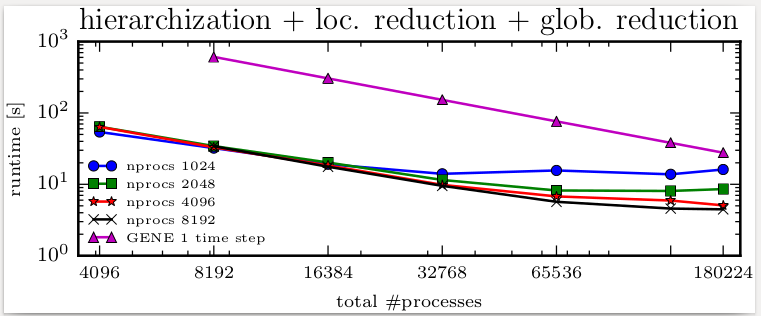
For the large-scale plasma turbulence simulations with GENE that
we aim for, a single component grid will be so large that it has to be computed
by a group of processes distributed over multiple nodes. In our latest works we in-
vestigated the combination of such distributed component grids. We present
experimental results that demonstrate the scalability of our combination al-
gorithm on up to 180,224 cores on the supercomputer Hazel Hen.
In our experiments we used 182 component grids that are computed on process
groups of up to 8,192 processes (each process group computes several compo-
nent grids one after each other). For the largest experiments we used 11 process
groups which had 8,192 processes each. Our recombination algorithm is fast
enough that it would even be possible to recombine a large GENE simulation
after each time step.
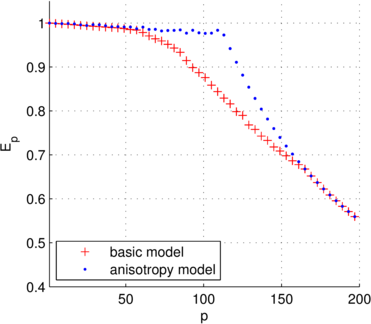
Exa-challenges and solutions: Load balancing
In order to perform effective load balancing with the combination technique, a load model to estimate the runtime of the partial solutions is required. However, to achieve a good estimate of the runtime, this means considering not only different problem sizes associated with the different partial grids, but also the anisotropy of the discretization. GENE, for example, treats the dimensions differently when choosing the optimal domain decomposition for a particular number of processes. This is due to the fact that not every dimension can be decomposed with the same granularity while ensuring a high degree of efficiency. Furthermore, depending on the mode of operation, the discretization has large effects on the underlying numerics. Thus we have to consider the anisotropy of each grid, which strongly influences the convergence rate and stability of the underlying numerical solvers. Variations in the degree of anisotropy result in variable number of linear solver iterations, and smaller timestep sizes are necessary for very anisotropic discretizations, even for comparable number of unknowns. In GENE, execution times may vary by more than a factor of three for partial solutions with about the same number of unknowns but different degrees of anisotropy.To address this issue, we developed a load model that attempts to estimate the execution time of a partial solution based on the number of unknowns and the anisotropy of the discretization. Using this model we were able to considerably increase the parallel efficiency of the second level of parallelization compared to a basic model that considers only the number of unknowns.
Exa-challenges and solutions: Fault tolerance
Through the joint collaboration with research associate Hegland's group in Australia, important steps have been taken in the development of the theory of a |
 |
 |
||
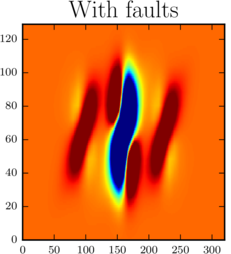
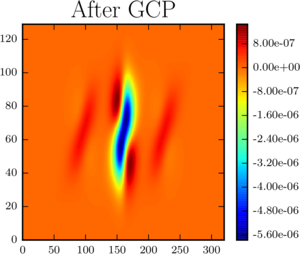
| GENE PDF: combination technique solution with 20 grids | GENE PDF: after 5 grids go missing | GENE PDF: recovery by FTCT, excluding failed grids |
 |
 |
|
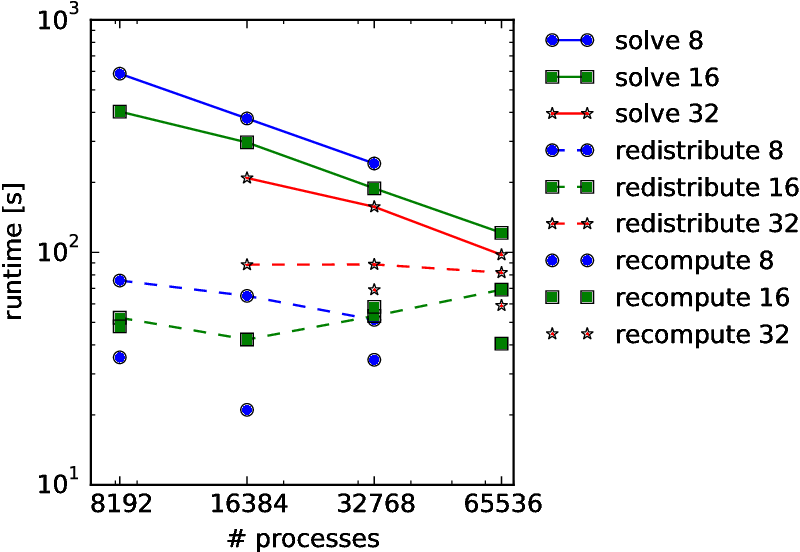
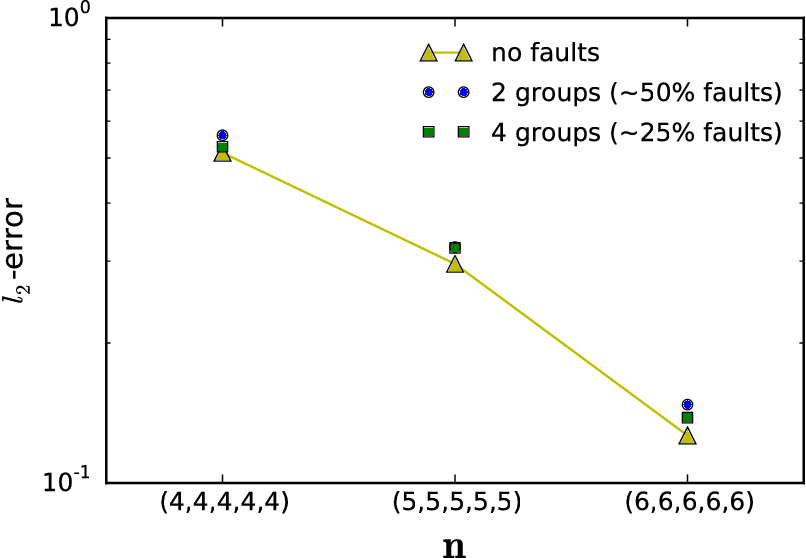
| Scaling experiments for a 5D combination technique with faults | Convergence of the combination solutoin after fault recovery |
The combination technique can also be used to detect
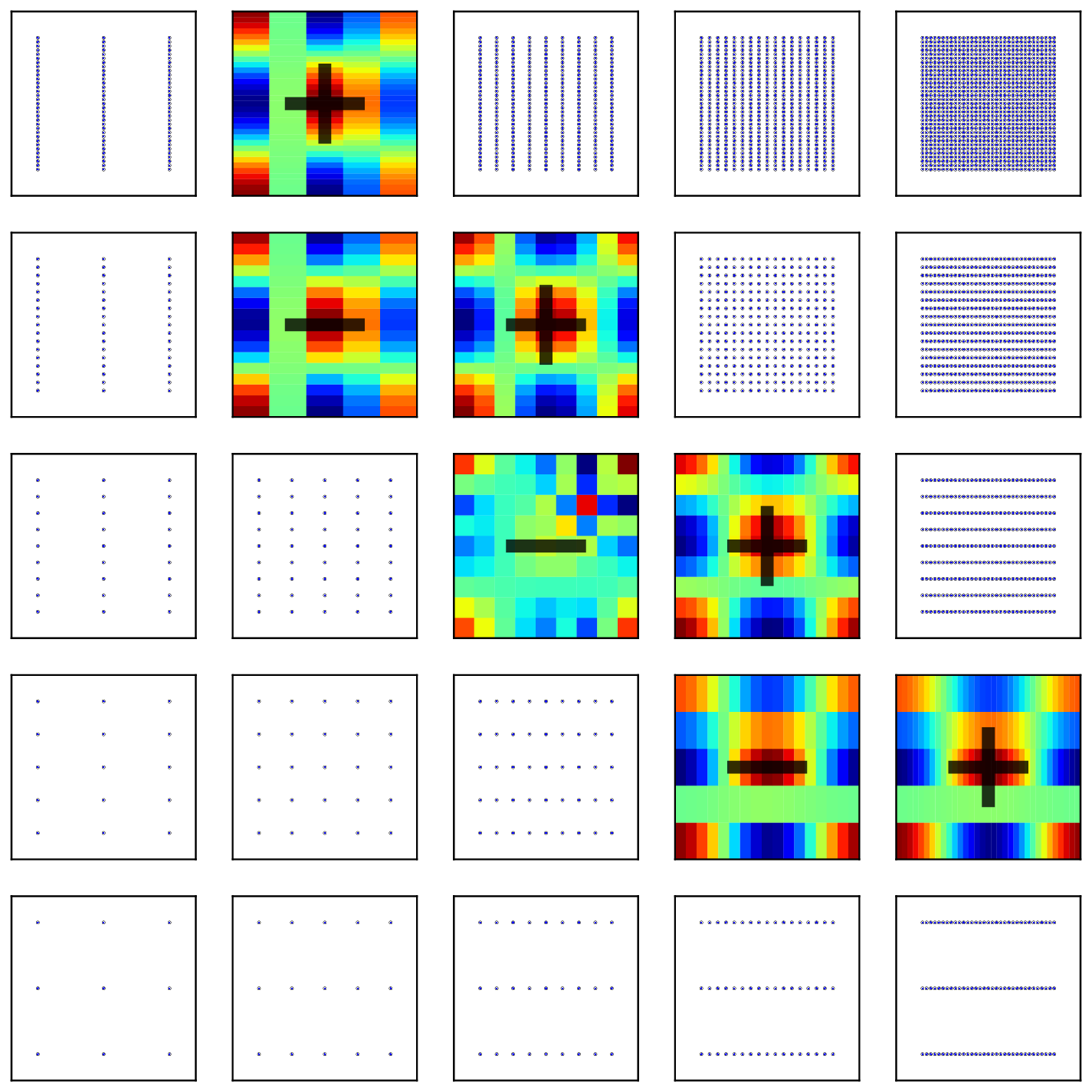 |
 |
 |
||
| One component solution affected by SDC | The resulting combination technique | Affected solutions can be detected |
Eigenvalue problems in GENE
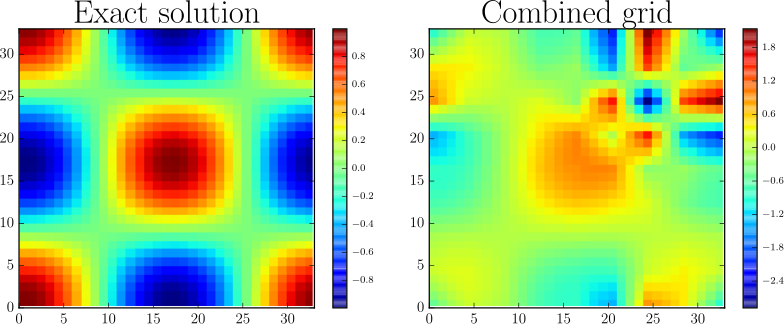
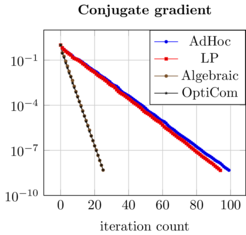
In the classical combination technique, the combination coefficients are fixed, which does not allow a direct combination of eigenmodes of GENE, since they are subject to a phase shift. We developed a new technique that does not rely on an operator bound norm. Instead, the eigenvalue problem is formulated as an optimization problem, in which the norm of the residual is minimized. The minimization adapts the combination coefficients. This so-called OptiCom method for eigenvalues not only combines the partial solutions to obtain a good approximation. It can also identify bad partial approximations, which can occur due to the anisotropic grids used, where some physical effects are not resolved well enough. With the OptiCom, these partial approximations obtain very small combination coefficients and they are thus effectively disregarded for the combined solution.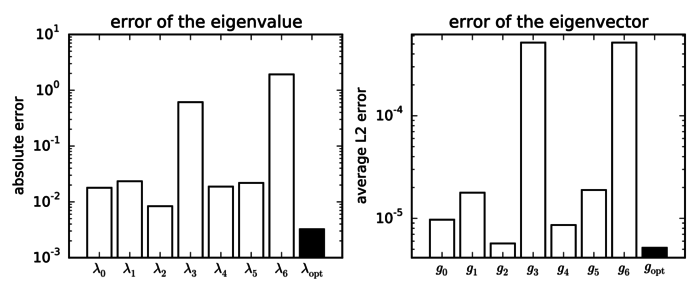
Numerics
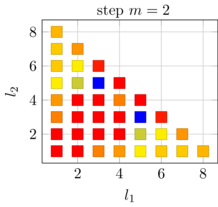
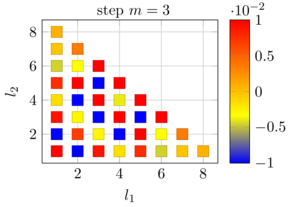
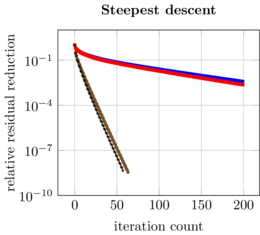
A crucial ingredient towards convergent and reliable numerical methods for high-dimensional problems in exascale computing is an in-depth theoretical and practical analysis of the proposed numerical techniques. While the ultimate objective is a deep theoretical understanding of the full application problem, we started the theoretical analysis with simplified model problems.Such a problem is the elliptic boundary value problem in weak formulation. While there is convergence theory for the solution of elliptic PDEs by sparse grid methods and by the sparse grid combination technique, the proposed iterated (optimized) combination technique has not been studied in theoretical and numerical terms, so far. Such an analysis has been achieved by PI Griebel and collaborators during the last year. Here, subspace correction approximations of higher-dimensional elliptic problems were carried out comparing the use of different scaling parameter approximations for the respective subspaces. It turned out that the iterated optimized combination technique is indeed an optimal candidate for approximations of higher-dimensional elliptic problems. The iterated
 |
 |
 |
 |
 |





